The relative importance of hardware and software progress: evidence from computer chess
September 2018
Summary
One topic within AI forecasting is: what is the relative importance of hardware and software to AI progress (Grace 2015, 2017)?
In order to make such forecasts, one option is to look at past events in a relevant reference class. In this document, I present new evidence on the relative importance of hardware and software in explaining the last 33 years of progress in computer chess. I construct and analyse a novel dataset using previously unexploited raw data of 54,919 games organised by the Swedish Computer Chess Association between 1985 and 2018.
This dataset contains instances of the same chess programme run on a range of hardware setups, as well as cases where a single piece of hardware was used to run many different programmes. This allows me to isolate the independent effect of hardware and software on performance.
One approach is to use dummy variables to directly capture the effect of each chess programme, controlling for clock speed. This approach estimates the effect of a clock speed doubling at 76 Elo. As for the dummy coefficients, they tell us, for example, that the software improvement from Fritz 1 to Deep Fritz 8 was 462 Elo. Further interpreting these numbers would require enough background knowledge of computer chess to develop an intuitive sense of how much intellectual progress particular algorithms represented.
A second approach introduces the date a programme was released as a variable, instead of dummies. Because I measure only a proxy for the date of release, this estimate is noisier, but it is more readily interpretable. The date-based estimate suggests that every additional year of chess programme development produces a gain of 10 to 20 Elo, while every clock speed doubling produces an increase of between 69 and 120 Elo, depending on the specification. In a CPU database covering 1971-2014, a clock speed doubling occurs every 3.46 years, suggesting that hardware has been roughly twice as important as software in explaining historical chess progress.
This echoes previous findings that ‘gains from algorithmic progress have been roughly fifty to one hundred percent as large as those from hardware progress’ (Grace 2013). However, the present report goes beyond previous analyses in two ways. First, it ensures that Elo score comparisons are meaningful by using data from a single chess rating list. In addition, it uses multiple regression to more systematically analyse a larger dataset covering a longer time period.
The Elo system
Performance in chess is traditionally measured using Elo scores. In the Elo system, according to Wikipedia,
Performance isn’t measured absolutely; it is inferred from wins, losses, and draws against other players. Players’ ratings depend on the ratings of their opponents, and the results scored against them. The difference in rating between two players determines an estimate for the expected score between them. […] A player’s expected score is their probability of winning plus half their probability of drawing.
If Player A has a rating of and player B a rating of , the expected score of Player A is .
When a player’s actual tournament scores exceed their expected scores, the Elo system takes this as evidence that player’s rating is too low, and needs to be adjusted upward. Similarly when a player’s actual tournament scores fall short of their expected scores, that player’s rating is adjusted downward. Elo’s original suggestion, which is still widely used, was a simple linear adjustment proportional to the amount by which a player overperformed or underperformed their expected score. The maximum possible adjustment per game, called the K-factor, was set at K = 16 for masters and K = 32 for weaker players.
Supposing Player A was expected to score points but actually scored points. The formula for updating their rating is .
This update can be performed after each game or each tournament, or after any suitable rating period. An example may help clarify. Suppose Player A has a rating of 1613, and plays in a five-round tournament. He or she loses to a player rated 1609, draws with a player rated 1477, defeats a player rated 1388, defeats a player rated 1586, and loses to a player rated 1720. The player’s actual score is (0 + 0.5 + 1 + 1 + 0) = 2.5. The expected score, calculated according to the formula above, was (0.51 + 0.69 + 0.79 + 0.54 + 0.35) = 2.88. Therefore, the player’s new rating is (1613 + 32(2.5 - 2.88)) = 1601, assuming that a K-factor of 32 is used. Equivalently, each game the player can be said to have put an ante of K times their score for the game into a pot, the opposing player also puts K times their score into the pot, and the winner collects the full pot of value K; in the event of a draw the players split the pot and receive K/2 points each.
Simpler approaches and why they fail
Approaches which use only variation in software cannot compare the effects of software and hardware
CCRL (Computer Chess Rating Lists) is an organisation that tests computer chess programmes’ strength by playing the programmes against each other. Each programme is given the same thinking time, or “time control”. On the CCRL 40/40 list, the programmes have the equivalent of 40 minutes for 40 moves on a AMD X2 4600+ processor at 2.4GHz. The programme Crafty 19.17 BH is run as a benchmark on the tester’s computer to determine the equivalent time control for their machine.
All programmes on the CCRL list use equivalent hardware, so any difference in their performance can be attributed to software. Grace (2013) writes:
To confirm that substantial software progress does occur, we can look at the CCRL (2013) comparison of Rybka engines. Rybka 1.1 64-bit was the best of its time (the year 2006), but on equivalent hardware to Rybka 4.1 it is rated 204 points worse (2,892 vs. 3,102)
So we can estimate the increase in Elo scores on the CCRL 40/40 list that is due to improvements in software. But we still don’t know how this compares to the improvements that have come from hardware. For this we need variation in both software and hardware. Furthermore, we need variation in both hardware and software within a single chess ratings list. It may not be valid to compare the Elo improvement from software in one list to the Elo improvement from hardware estimated from a different list1. This is because Elo scores cannot be directly compared across lists. The Elo system only measures the relative performance of players. In human FIDE (World Chess Federation) chess, Elo ratings are able to be calibrated on a single scale, because the same humans play under identical conditions across different tournaments (there is a single time control for all major FIDE events). According to Wikipedia, computer chess rating lists have no direct relation to FIDE Elo ratings:
there is no calibration between any of these [computer] rating lists and [human] player pools. Hence, the results which matter are the ranks and the differences between the ratings, and not the absolute values. Also, each list calibrates their Elo via a different method. Therefore, no Elo comparisons can be made between the lists.
For example, in the CCRL 40/4 list, the top rated programme has an Elo of 3560, while the current champion of the 40/40 list, which allows 10 times more thinking time, has an Elo of only 3439.
Estimating software progress as what is left unexplained by hardware suffers from omitted variable bias
Supposing we had data from a single ratings list with variation in both software and hardware, we might reason as follows. A chess programme is a piece of software run on some hardware, so hardware and software are jointly exhaustive categories of inputs to chess performance. Hence whatever difference in performance isn’t explained by hardware must be due to software, and vice versa. One could run a regression of Elo scores on some measure(s) of hardware (say, processor clock speed and RAM), the residuals of which would be a hardware-adjusted Elo score. Any change in hardware-adjusted Elo scores would be due to software. However, this line of reasoning is flawed. Hardware is not exogenously determined, it is correlated with the residual “software” term in the regression. Modern chess programmes are run on much better hardware, So the regression would suffer from omitted variable bias in the direction of overestimating the effect of hardware.
This document’s approach
The SSDF dataset
On computer chess ranking lists, hardware is usually scrupulously standardised in order to compare chess programmes in the fairest way possible.
I could find only one source of data in which hardware varies: the SSDF (Swedish Computer Chess Association) list, which records chess games since 1985 and has changed its hardware several times. I process and merge SSDF’s raw data to produce a novel dataset of 366 programmes-hardware pairs and their Elo ratings. The data methods are detailed in section 5.
Measuring software
If we want to include software as an independent variable, we need to measure the “quality of software” of each chess programme in a meaningful and interpretable way. I use two different approaches.
Using programme dummies
When SSDF changed their hardware in 2008, they commented2:
Six [programmes] have been tested on both Q6600 and Athlon 1200 MHz, which makes a comparison possible. The total effect of a faster processor, four instead of one CPU and the use of 64-bit operating system instead of 32 bit has in average given a rating increase of 120 points. Deep Fritz 8 gained the most with 142 points whereas Deep Junior 8 increased the least with 84 points.
This example allows us to compare the gains due to hardware (Athlon to Q6600) to the gains due to software (e.g. Deep Fritz 8 to Deep Rybka 3). We have a 2x2 table of Elo scores:
| Q6600 | Athlon | |
| Deep Rybka 3 | 3193 | 3075 |
| Deep Fritz 8 | 2898 | 2781 |
The generalisation of this approach is to conduct a regression in which dummy variables are created for programmes in the dataset. This allows us to quantify the effect of moving from some “baseline programme” (which has no dummy) to any other programme, controlling for hardware.
I am able to identify 46 instances where a programme was used on more than one hardware configuration, totalling 96 data points (because four programmes were used on three configurations). Out of these, 82 have clock speed data available3. I use the natural log of clock speed throughout, in keeping with Moore’s law. I use Fritz 1 as the baseline programme.
Table 1 presents the results. As expected, this regression explains virtually all the variation, since hardware and software are jointly exhaustive categories of computer chess inputs. The regression coefficient on clock speed is estimated with very high precision.
Since we are using log clock speed, the interpretation of the coefficient is that for every clock speed doubling, . This is about the same as the difference between Conchess Glasgow and Fritz 1. For comparison, data from the Stanford CPU Database (Danowitz et al. 2012), which covers 1971-2014, suggests that a clock speed doubling has historically occurred every 3.46 years.
We can see the progression of the Fritz engines, controlling for clock speed:
| Improvement from Fritz 1 | Release Date | |
| Fritz 1 | 0 | 1992 |
| Fritz 3 | 192 | 1995 |
| Deep Fritz | 395 | 2000 |
| Deep Fritz 7 | 428 | 2002 |
| Deep Fritz 8 | 462 | 2004 |
The Fritz line of software has improved by about 39 Elo per year on average, suggesting that software has been responsible for almost twice as much progress as hardware when it comes to Fritz.

Using the date of release
Another approach is to use the release date of a programme as a (very noisy) measure of the amount of developer effort that went into its design. There are two main advantages to this approach. First, more data is available since we are not restricted to instances where a programme was used on more than one hardware configuration. Second, the regression coefficient is easily interpretable as measuring the effect of one year of computer chess development on performance. The main disadvantage is the noisiness of the proxy.
To approximate the release date of a programme, I use the date at which the programme was first played in an SSDF game. The approximation is very good for the most part, except in some cases where the organisers intentionally test very old “legacy” programmes on new hardware for the first time.
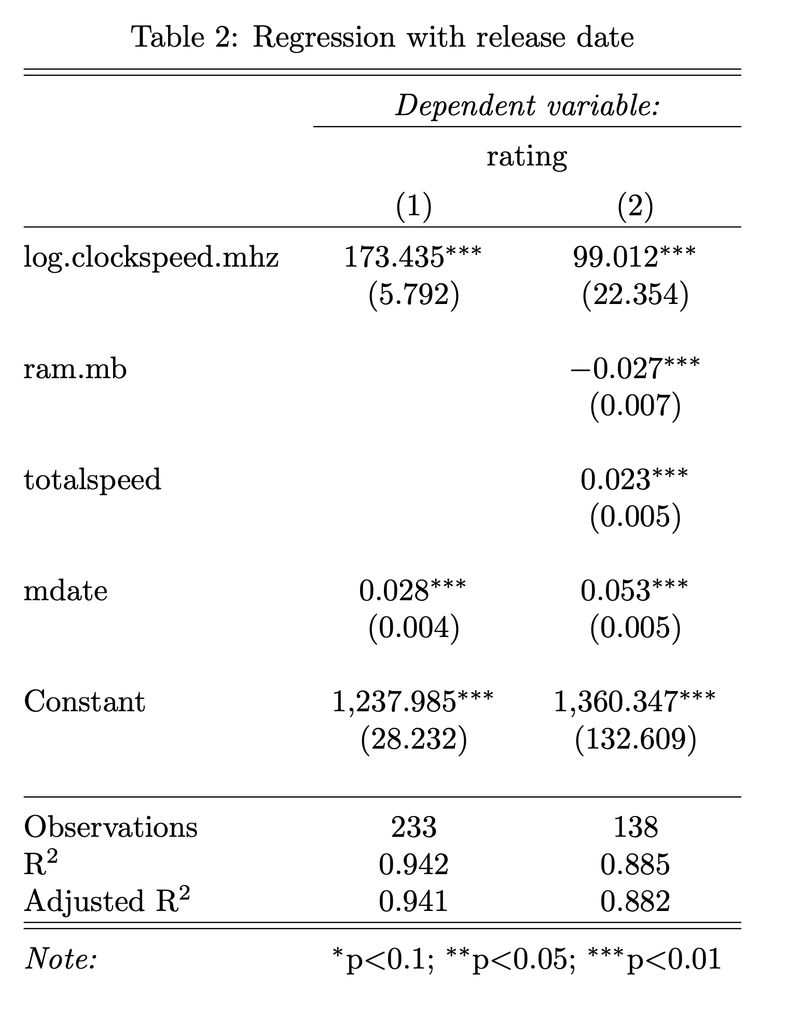
I conduct two regressions, presented in Table 2. Regression (1) () uses release date and clock speed only. Regression (2) () employs a finer-grained measure of hardware that includes clock speed, RAM, and the product of clock speed and number of cores (total speed). All coefficients are estimated with very high statistical precision.
It appears that after accounting for clock speed, the number of cores tells us little about performance, while the coefficient on RAM is actually small and negative. This could be because the small amount variation in RAM and the number of cores in this dataset (see section 5.2.3) is highly correlated with changed in clock speed. The effect of clock speed is of similar magnitude to that found using dummies: between 69 and 120 Elo per doubling. The effect of the release date is between 10 and 20 Elo points per year. Recall that a clock speed doubling has historically occurred every 3.46 years (Danowitz et al. 2012). This would suggest that hardware has mattered roughly twice as much as software for progress in computer chess.
Data processing methods
Sourcing and importing the data
SSDF ranking
The file ssdf-summary-data-original.txt contains the current rating of
366 programme-hardware pairs in tab-separated plain text format, as well
as information on hundreds of games. I truncate the file to retain only
the ranked list, and convert it to CSV ssdf-summary-data-clean.csv. I
call this dataset su.
SSDF data on 54,919 games
I download the plain-text database SSDF.PGN, which fully describes
each of the 54,919 games (including every move made by each player). An
example entry:
[Event "Testspel av Tony Hed"]
[Site "?"]
[Date "1992.01.01"]
[Round "?"]
[White "Fritz 1 486/33 MHz"]
[Black "Mephisto Academy 6502 5 MHz"]
[Result "0-1"]
[ECO "A28"]
[PlyCount "83"]
1. c4 e5 2. Nc3 Nf6 3. Nf3 Nc6 4. d4 e4 5. Ng5 h6 6. Ngxe4 Nxe4 7. Nxe4 Qh4 8. Nc3 Qxd4 9. e3 Qxd1+ 10. Kxd1 Be7 11. Nd5 Bd8 12. Be2 O-O 13. Bd2 d6 14. Bc3 Ne5 15. Ba5 c6 16. Bxd8 Rxd8 17. Ne7+ Kh7 18. Nxc8 Raxc8 19. Ke1 d5 20. b3 dxc4 21. Bxc4 Rc7 22. Rd1 Rxd1+ 23. Kxd1 Rd7+ 24. Kc2 Nxc4 25. bxc4 Kg6 26. Rd1 Rxd1 27. Kxd1 Kf5 28. Ke2 c5 29. h3 a6 30. Kd3 b5 31. f4 g5 32. g3 bxc4+ 33. Kxc4 g4 34. e4+ Kxe4 35. hxg4 f6 36. Kxc5 Kf3 37. g5 hxg5 38. Kd5 Kxg3 39. fxg5 fxg5 40. Kc5 g4 41. Kb6 Kf4 42. Kxa6 0-1
I write the python script extract-earliest-dates.py, which uses
regular expressions to clean up the file. In the resulting
output3.txt, there is one line for every game; each lines gives the
date and the programme-hardware pair which played White, separated by a
comma. I call this data full.
Data analysis in R
Cleaning both data sets
All subsequent data cleaning and analysis are conducted in r.R. In the
source data, the software-hardware pairs are in unstructured plain text.
For example:
Rebel Century 3 K6-2 450 MHz
P.Fritz 3 Glaurung 2.1 PXA270 520 MHz
Pocket Fritz 2 Shredder PXA255 400 MHz
Goliath Light K6-2 450 MHz
Fritz 5.32 64MB P200 MHz MMX
Crafty 17.07 CB K6-2 450 MHz
Nimzo 99 K6-2 450 MHz
Resurrection Rybka 2.2 ARM 203 MHz
MChess Pro 8 K6-2 450 MHz
Genius 6.5 K6-2 450 MHz
Chessmaster 6000 64MB P200 MHz MMX
Hiarcs 7.32 64MB P200 MHz MMX
Fritz 5 PB29% 67MB P200 MHz MMX
ChessGenius 3 ZTE Apex3 ARM A53 1.3 GHz
Fritz 4 Pentium 90 MHz
Kallisto 1.98 Pentium 90 MHz
MChess Pro 5 486/50-66 MHz
Rebel 7 486/50-66 MHz
Significant data cleaning is required. I define 5 functions using
regular expressions, which are applied in the order below. For
consistency, I apply the same functions to both su and full.
-
extract_clock_speeds()uses two different methods. First, it matches strings of the form2.4 GHzwhere a decimal number is followed byGHzorMHz. Second, it captures anything to the right of a processor (seeextract_processors()below), since clock speeds are usually given immediately after the name of the processor. -
clean_clock_speeds()removes extraneous characters and turns strings withGHzandMHzinto numeric values in MHz. -
extract_processors()catches anything that matches a manually collected list of 32 processors. -
standardise_progs()removes whitespace and trailing zeroes. Next, and somewhat contentiously, it removesx64andMP(“multi-processor”). This is because these labels are inconsistently applied between the two datasets, and to my understanding also withinSSDF.PGN. Keeping these labels would make merging much more difficult, and the date-based analysis relies crucially on merging datasets. For the dummies analysis, the choice is less defensible, but allows much more data to be used. The hope is that there is not too much difference between the x64 and MP versions and other versions of a single programme. If I did further work with this data, I would look at the impact of these choices on the results. -
clean_progs()removes extraneous characters
Processing full
full contains missing dates, indicated using question marks. The
function unknown_date_default() deals with missing values in the
following way:
-
An unknown year defaults to 2100, since we are only interested in the earliest appearance of an programme
-
An unknown month or day defaults to
01(the more principled choice would be31for a missing day and12for a missing month, but this would require a more cumbersome regular expression, and I don’t need that much precision)
Then I drop all observations that are not the earliest appearance of an programme. I also remove games that are claimed to have occurred in 1900.
Imputing RAM and number of cores
The number of cores in a processor, and the amount of RAM on the
computer that was used for a game are usually not given in the source
data (only the clock speed is). This data needs to be added manually. On
hardware.htm, the following is written:
The hardware of the different hardware levels:
Intel Pentium 90 MHz - 8-16 MB RAM
Intel Pentium 200 MHz MMX - 32-64 MB RAM
AMD K6-2 450 MHz - Single processor, 32 bit OS, 128 MB RAM, 5 piece TableBases on HHD
AMD Athlon Thunderbird 1200 MHz - Single processor, 32 bit OS, 256 MB RAM, 5p TB on HHD
Intel Core2Quad Q6600 2400 MHz - Quad Core processor, 64 bit OS, 2 GB RAM, 5p TB on HHD
AMD Ryzen 7 1800X 3600 MHz - Octa Core processor, 64 bit OS, 16 GB RAM, 6p Syzygy on SSD (or 5p Nalimov on SSD)
I manually write this in
processor-info.csv, to be merged later. Further work on this could involve digging up more such information. Sometimes, when a new version of the list is released, SSDF adds a comment oncomment.htm. I have extracted all such comment pages from the internet archive, they can be found in the directorydatacomments. I have not studied them, but more information on the hardware setups that were historically used could be hidden there.
Merging
For the date-based analysis, I now finally merge su and full,
matching by the programme name. I also merge the imputed information in
ramcores.
For the dummies analysis, I only merge ramcores.
When information on the number of cores is available, I compute the clock speed times the number of cores, which is the total number of operations per second available to the processor.
Further data
I use the Ruby script mayback_machine_downloader (Hartator 2018) to
pull all versions of the entire SSDF site stored on the Web Archive. I
have not yet done anything with this data.
When analysing the Stanford CPU database (Danowitz et al. 2012), I use
only the summary file processor.csv. I simply regress the date on the
natural log of clock speed. Then I multiply the coefficient by
and divide by .
References
-
To the extent that Elos from different lists are not comparable, analyses such as that in section 5.1.3 of Grace (2013) would be invalidated. ↩
-
See
datacomments/comment_003.htm↩ -
I do not use the RAM and cores data I have collected (see section 5), since this would reduce the number of data points even more, but such a regression could easily be conducted. ↩