This is part of my series on success stories in philosophy. See this page for an explanation of the project and links to other items in the series.

Contents

1. Contents
2. Background
3. The problem of multiple generality
   1. How people were confused (a foray into the strange world of suppositio)
   2. How predicate logic dissolved the confusion
4. Definite descriptions
   1. How people were confused
   2. How predicate logic dissolved the confusion
5. The epsilon-delta definition of a limit
   1. How people were confused
   2. How predicate logic dissolved the confusion
6. On the connection between the analysis of definite descriptions and that of limit
7. “That depends what the meaning of ‘is’ is”

Background

Frege “dedicated himself to the idea of eliminating appeals to intuition in the proofs of the basic propositions of arithmetic”. For example:

A Kantian might very well simply draw a graph of a continuous function which takes values above and below the origin, and thereby ‘demonstrate’ that such a function must cross the origin. But both Bolzano and Frege saw such appeals to intuition as potentially introducing logical gaps into proofs.

In 1872, Weierstrass described a real-valued function that is continuous everywhere but differentiable nowhere. All the mathematics Weierstrass was building on had been established by using “obvious” intuitions. But now, the intuitive system so built up had led to a highly counter-intuitive result. This showed that intuitions can be an unreliable guide: by the lights of intuition, Weierstrass’s result introduced a contradiction in the system. So, Frege reasoned, we should ban intuitive proof-steps in favour of a purely formal system of proof. This formal system would (hopefully) allow us to derive the basics propositions of arithmetic. Armed with such a system, we could then simply check whether Weierstrass’s result, and others like it, hold or not.

So Frege developed predicate logic. In what follows I’ll assume familiarity with this system.

While originally developed for this mathematical purpose, predicate logic turned out to be applicable to a number of philosophical issues; this process is widely considered among the greatest success stories of modern philosophy.

The problem of multiple generality

How people were confused (a foray into the strange world of suppositio)

Dummett 1973:

Aristotle and the Stoics had investigated only those inferences involving essentially sentences containing not more than one expression of generality.

Aristotle’s system, which permits only four logical forms, seems comically limited¹ by today’s standards, yet Kant “famously claimed, in Logic (1800), that logic was the one completed science, and that Aristotelian logic more or less included everything about logic there was to know.” (Wikipedia).

Some medieval logicians attempted to go beyond Aristotle and grappled with the problem of multiple generality. As Dummet writes (my emphasis),

Scholastic logic had wrestled with the problems posed by inferences depending on sentences involving multiple generality – the occurrence of more than one expression of generality. In order to handle such inferences, they developed ever more complex theories of different types of ‘suppositio’ (different manners in which an expression could stand for or apply to an object): but these theories, while subtle and complex, never succeeded in giving a universally applicable account.
It is necessary, if Frege is to be understood, to grasp the magnitude of the discovery of the quantifier-variable notation, as thus resolving an age-old problem the failure to solve which had blocked the progress of logic for centuries. […] for this resolved a deep problem, on the resolution of which a vast area of further progress depended, and definitively, so that today we are no longer conscious of the problem of which it was the solution as a philosophical problem at all.

Medieval philosophers got themselves into terrible depths of confusion when trying to deal with these sentences having more than one quantifier. For example, from “for each magnitude, there is a smaller magnitude”, we want to validate “each magnitude is smaller than at least one magnitude” but not “there is a magnitude smaller than every magnitude”. The medievals analysed this in terms of context-dependence of the meanings of quantified terms:

The general phenomenon of a term’s having different references in different contexts was called suppositio (substitution) by medieval logicians. It describes how one has to substitute a term in a sentence based on its meaning—that is, based on the term’s referent. (Wikipedia)

The scholastics specified many different types of substitution, and which operations were legitimate for each; but never progressed beyond a set of ham-fisted, ad-hoc rules.

To show examples, I had to go to modern commentaries of the scholastics, since the actual texts are simply impenetrable.

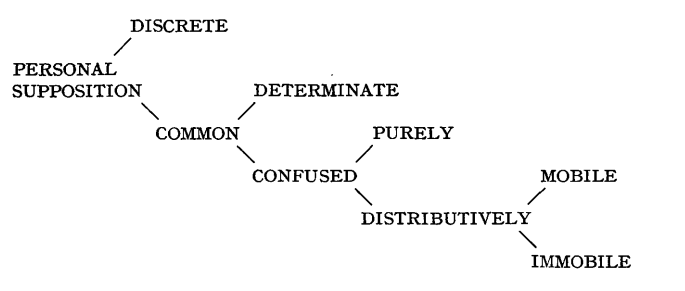
Swiniarski 1970. Ockham’s Theory of Personal Supposition

Broadie 1993, which is Oxford University Press’ Introduction to medieval logic:

a term covered immediately by a sign of universality, for example, by ‘all’ or ‘every’, has distributive supposition, and one covered mediately by a sign of affirmative universality has merely confused supposition. A term is mediately covered by a given sign if the term comes at the predicate end of a proposition whose subject is immediately covered by the sign. Thirdly, a term covered, whether immediately or mediately, by a sign of negation has confused distributive supposition (hereinafter just ‘distributive supposition’). Thus in the universal negative proposition ‘No man is immortal’, both the subject and the predicate have distributive supposition, and in the particular negative proposition ‘Some man is not a logician’, the predicate has distributive supposition and the subject has determinate supposition. […]

Given the syntactic rules presented earlier for determining the kind of supposition possessed by a given term, it follows that changing the position of a term in a proposition can have an effect on the truth value of that proposition. In:

(10) Every teacher has a pupil

‘pupil’ has merely confused supposition, and consequently the proposition says that this teacher has some pupil or other and that teacher has some pupil or other, and so on for every teacher. But in:

(11) A pupil every teacher has

‘pupil’ has determinate supposition, and since ‘teacher’ has distributive supposition descent must be made first under ‘pupil’ and then under ‘teacher’. Assuming there to be just two teachers and two pupils, the first stage of descent takes us to:

(12) PupiI1 every teacher has or pupil2 every teacher has.

The next stage takes us to:

(13) Pupil1 teacher1 has and pupil1 teacher2 has, or pupil2 teacher1 has and pupil2 teacher2 has.

(13) implies that some one pupil is shared by all the teachers, and that is plainly not implied by (10), though it does imply (10).

In all this talk of supposition, we can discern a flailing attempt to deal with ambiguities of quantifier scope, but these solutions are, of course, hopelessly ad hoc. Not to mention that the rules of supposition were in flux, and their precise content is still a matter of debate among specialists of Scholasticism².

And now just for fun, a representative passage from Ockham:

And therefore the following rule can be given concerning negations of this kind : Negation which mobilizes what is immobile, immobilizes what is mobile, that is, when such a negation precedes a term which supposits determinately it causes the term to supposit in a distributively confused manner, and when it precedes a term suppositing in a distributively confused manner it causes the term to supposit determinately.

According to one commentator (Swiniarski 1970), in this passage “Ockham formulates a De Morgan-like rule concerning the influence of negations which negate an entire proposition and not just one of the terms.” I’ll let you be the judge. For at this point it is I who supposit in a distributively confused manner.

How predicate logic dissolved the confusion

The solution is now familiar to anyone who has studied logic. Wikipedia gives a simple example:

Using modern predicate calculus, we quickly discover that the statement is ambiguous. “Some cat is feared by every mouse” could mean

• For every mouse m, there exists a cat c, such that c is feared by m, i.e. $\forall m (M(m) \rightarrow \exists c (C(c) \land F(m,c)))$

But it could also mean

• there exists one cat c, such that for every mouse m, c is feared by m, i.e. $\exists c (C(c) \land \forall m (M(m) \rightarrow F(m,c))$.

Of course, this is only the simplest case. Predicate logic allows arbitrarily deep nesting of quantifiers, helping us understand sentences which the scholastics could not even have made intuitive sense of, let alone provide a formal semantics for.

Definite descriptions

How people were confused

The problem here is with sentences like “Unicorns have horns” which appear to refer to non-existent objects. People were quite confused about them:

Meinong, an Austrian philosopher active at the turn of the 20th century, believed that since non-existent things could apparently be referred to, they must have some sort of being, which he termed sosein (“being so”). A unicorn and a pegasus are both non-being; yet it’s true that unicorns have horns and pegasi have wings. Thus non-existent things like unicorns, square circles, and golden mountains can have different properties, and must have a ‘being such-and-such’ even though they lack ‘being’ proper. The strangeness of such entities led to this ontological realm being referred to as “Meinong’s jungle”. (Wikipedia)

The delightfully detailed Stanford page on Meinong provides further illustration:

Meinong tries to give a rational account of the seemingly paradoxical sentence “There are objects of which it is true that there are no such objects” by referring to two closely related principles: (1) the “principle of the independence of so-being from being” [“Prinzip der Unabhängigkeit des Soseins vom Sein”], and (2) the “principle of the indifference of the pure object to being” (“principle of the outside-being of the pure object” [“Satz vom Außersein des reinen Gegenstandes”]) (1904b, §3–4). […]

Meinong repeatedly ponders the question of whether outside-being is a further mode of being or just a lack of being (1904b, §4; 1910, §12; 1917, §2; 1978, 153–4, 261, 358–9, 377). He finally interprets outside-being as a borderline case of a kind of being. Every object is prior to its apprehension, i.e., objects are pre-given [vorgegeben] to the mind, and this pre-givenness is due do the (ontological) status of outside-being. If so, the most general determination of so-being is being an object, and the most general determination of being is outside-being. The concept of an object cannot be defined in terms of a qualified genus and differentia. It does not have a negative counterpart, and correlatively outside-being does not seem to have a negation either (1921, Section 2 B, 102–7).

In fact, as John P. Burgess writes:

as Scott Soames reveals, in his Philosophical Analysis in the Twentieth Century, volume I: The Dawn of Analysis, Russell himself had briefly held a similar view [to Meinong’s]. It was through the development of his theory of descriptions that Russell was able to free himself from anything like commitment to Meinongian “objects.”

How predicate logic dissolved the confusion

Russell’s On denoting, as the most famous case of a solved philosophical problem, needs no introduction. (Wikipedia gives a good treatment, and so does Sider’s Logic for Philosophy, section 5.3.3.)

Russell’s analysis of definite descriptions could have stood on its own as a success story. The tools of predicate logic were not, strictly speaking, necessary to discover the two possible interpretations of empty definite descriptions. In fact it may seem surprising that no-one made this discovery earlier. But as literate people of the 21st century, it can be hard for us to imagine the intellectual poverty of a world without predicate logic. So we must not be too haughty. The most likely conclusion, it seems to me, is that Russell’s insight was, in fact, very difficult to achieve without the precision afforded by Frege’s logic.

The epsilon-delta definition of a limit

How people were confused

As Wikipedia writes:

The need for the concept of a limit came into force in the 17th century when Pierre de Fermat attempted to find the slope of the tangent line at a point $x$ of a function such as $f(x)=x^{2}$. Using a non-zero, but almost zero quantity, $E$, Fermat performed the following calculation:

$$\begin{aligned} slope &= \frac{f(x+E)-f(x)}{E} \\ &= \frac{x^2 +2xE + E^2 -x^2}{E} \\ &= 2x + E \\ &= 2x \end{aligned}$$

The key to the above calculation is that since $E$ is non-zero one can divide $f(x+E)-f(x)$ by $E$, but since $E$ is close to $0$, $2x+E$ is essentially $2x$. Quantities such as $E$ are called infinitesimals. The problem with this calculation is that mathematicians of the era were unable to rigorously define a quantity with properties of $E$ although it was common practice to ‘neglect’ higher power infinitesimals and this seemed to yield correct results.

SEP states:

Infinitesimals, differentials, evanescent quantities and the like coursed through the veins of the calculus throughout the 18th century. Although nebulous—even logically suspect—these concepts provided, faute de mieux, the tools for deriving the great wealth of results the calculus had made possible. And while, with the notable exception of Euler, many 18th century mathematicians were ill-at-ease with the infinitesimal, they would not risk killing the goose laying such a wealth of golden mathematical eggs. Accordingly they refrained, in the main, from destructive criticism of the ideas underlying the calculus. Philosophers, however, were not fettered by such constraints. […]

Berkeley’s arguments are directed chiefly against the Newtonian fluxional calculus. Typical of his objections is that in attempting to avoid infinitesimals by the employment of such devices as evanescent quantities and prime and ultimate ratios Newton has in fact violated the law of noncontradiction by first subjecting a quantity to an increment and then setting the increment to 0, that is, denying that an increment had ever been present. As for fluxions and evanescent increments themselves, Berkeley has this to say:

And what are these fluxions? The velocities of evanescent increments? And what are these same evanescent increments? They are neither finite quantities nor quantities infinitely small, nor yet nothing. May we not call them the ghosts of departed quantities?

Kline 1972 also tells us:

Up to about 1650 no one believed that the length of a curve could equal exactly the length of a line. In fact, in the second book of La Geometrie, Descartes says the relation between curved lines and straight lines is not nor ever can be known.

How predicate logic dissolved the confusion

Simply let $f$ be a real-valued function defined on $\mathbb{R}$. Let $c$ and $L$ be real numbers. We can rigorously define a limit as:

$$\lim_{x \rightarrow c}=L \leftrightarrow (\forall \varepsilon > 0, \exists \delta >0, \forall x \in \mathbb{R}, 0<|x-c|<\delta \rightarrow |f(x)-L|<\varepsilon)$$

From this it’s easy to define the slope as the limit of a rate of increase, to define continuity, and so on.

Note that there are two nested quantifiers here, and an implication sign. When we remind ourselves how much confusion just one nested quantifier caused ante-Frege, it’s not surprising that this new definition was not discovered prior to the advent of predicate logic.

On the connection between the analysis of definite descriptions and that of limit

John P. Burgess, in The Princeton companion to mathematics, elaborates on the conceptual link between these two success stories:

[Definite descriptions] illustrate in miniature two lessons: first, that the logical form of a statement may differ significantly from its grammatical form, and that recognition of this difference may be the key to solving or dissolving a philosophical problem; second, that the correct logical analysis of a word or phrase may involve an explanation not of what that word or phrase taken by itself means, but rather of what whole sentences containing the word or phrase mean. Such an explanation is what is meant by a contextual definition: a definition that does not provide an analysis of the word or phrase standing alone, but rather provides an analysis of contexts in which it appears.

In the course of the nineteenth-century rigorization, the infinitesimals were banished: what was provided was not a direct explanation of the meaning of $df (x)$ or $dx$, taken separately, but rather an explanation of the meaning of contexts containing such expressions, taken as wholes. The apparent form of $df (x)/dx$ as a quotient of infinitesimals $df (x)$ and $dx$ was explained away, the true form being $(d/dx)f (x)$, indicating the application of an operation of differentiation $d/dx$ applied to a function $f (x)$.

“That depends what the meaning of ‘is’ is”

Bill Clinton’s quote has become infamous, but he’s got a point. There are at least four meanings of ‘is’. They can bec clearly distinguished using predicate logic.

Hintikka ‎2004:

Perhaps the most conspicuous feature that distinguishes our contemporary « modern » logic created by Frege, Peirce, Russell and Hilbert from its predecessors is the assumption that verbs for being are ambiguous between the is of predication (the copula), the is of existence, the is of identity, and the is of subsumption. This assumption will be called the Frege-Russell ambiguity thesis. This ambiguity thesis is built into the usual notation of first-order logic and more generally into the usual notation for quantifiers of any order, in that the allegedly different meanings of verbs like « is » are expressed differently in it. The is of existence is expressed by the existential quantifier (\exists x), the is of predication by juxtaposition (or, more accurately speaking, by a singular term’s filling the argument slot of a predicative expression), the is of identity by = , and the is of subsumption by a general conditional.