Monadic predicate logic (with identity) is decidable. (See Boolos, Burgess, and Jeffrey 2007, Ch. 21. The result goes back to Löwenheim-Skolem 1915).

How can we write a program to check whether a formula is logically valid (and hence also a theorem)?

First, we have to parse the formula, meaning to convert it form a string into a format that represents its syntax in a machine-readable way. That format is an abstract syntax tree like this:

Formula:
∀x(Ax→(Ax∧Bx))

Abstract syntax tree:
∀
├── x
└── →
    ├── A
    │   └── x
    └── ∧
        ├── A
        │   └── x
        └── B
            └── x

Writing the parser was a fun lesson in a fundamental aspect of computer science. But there was nothing novel about this exercise, and not much interesting to say about it.

The focus of this post, instead, is the part of the program that actually checks whether this syntax tree represents a logically valid formula.

To start with, we might try to evaluate the formula under every possible model of a given size. How big does the model need to be?

We can make use of the Löwenheim-Skolem theorem (looking first at the case without identity):

If a sentence of monadic predicate logic (without identity) is satisfiable, then it has a model of size no greater than $2^k$, where $k$ is the number of predicates in the sentence. (Lemma 21.8 BBJ).

A sentence’s negation is satisfiable if and only if the sentence is not valid, so the theorem equivalently states: a sentence is valid iff it is true under every model of size no greater than $2^k$.

For a sentence with $k$ predicates, every constant $c$ in the model is assigned a list of $k$ truth-values, representing for each predicate $P$ whether $P(c)$. We can use itertools to find every possible such list, i.e. every possible assignment to a constant.

>>> k = 2
>>> possible_predicate_combinations = [i for i in itertools.product([True,False],repeat=k)]
[(True, True), (True, False), (False, True), (False, False)]

The list of every possible assignment to a constant has a length of $2^k$.

We can then ask itertools to give us, for a model of size $m$, every possible combination of $m$ such lists of possible constant-assignments. We let $m$ be at most $2^k$, because of the theorem.

>>> for m in range(1,2**k+1):
>>>     possible_models = [i for i in itertools.product(possible_predicate_combinations,repeat=m)]
>>>     print(len(possible_models),"possible models of size",m)
>>>     for model in possible_models:
>>>         print(list(model))

4 possible models of size 1
[(True, True)]
[(True, False)]
[(False, True)]
[(False, False)]

16 possible models of size 2
[(True, True), (True, True)]
[(True, True), (True, False)]
[(True, True), (False, True)]
[(True, True), (False, False)]
[(True, False), (True, True)]
[(True, False), (True, False)]
[(True, False), (False, True)]
[(True, False), (False, False)]
[(False, True), (True, True)]
[(False, True), (True, False)]
[(False, True), (False, True)]
[(False, True), (False, False)]
[(False, False), (True, True)]
[(False, False), (True, False)]
[(False, False), (False, True)]
[(False, False), (False, False)]

64 possible models of size 3
[(True, True), (True, True), (True, True)]
[(True, True), (True, True), (True, False)]
[(True, True), (True, True), (False, True)]
[(True, True), (True, True), (False, False)]
[(True, True), (True, False), (True, True)]
[(True, True), (True, False), (True, False)]
[(True, True), (True, False), (False, True)]
[(True, True), (True, False), (False, False)]
[(True, True), (False, True), (True, True)]
[(True, True), (False, True), (True, False)]
...

256 possible models of size 4
[(True, True), (True, True), (True, True), (True, True)]
[(True, True), (True, True), (True, True), (True, False)]
[(True, True), (True, True), (True, True), (False, True)]
[(True, True), (True, True), (True, True), (False, False)]
[(True, True), (True, True), (True, False), (True, True)]
[(True, True), (True, True), (True, False), (True, False)]
[(True, True), (True, True), (True, False), (False, True)]
[(True, True), (True, True), (True, False), (False, False)]
[(True, True), (True, True), (False, True), (True, True)]
[(True, True), (True, True), (False, True), (True, False)]
...

What’s unfortunate here is that for our $k$-predicate sentence, we will need to check $\sum_{m=1}^{2^k} (2^k)^m =\frac{2^k ((2^k)^{2^k} - 1)}{2^k - 1}$ models. The sum is very roughly equal to its last term, $(2^k)^{2^k} = 2^{k2^k}$. For $k=3$, this is a number in the billions, for $k=4$, it’s a number with 19 zeroes.

So checking every model is computationally impossible in practice. Fortunately, we can do better.

Let’s look back at the Löwenheim-Skolem theorem and try to understand why $2^k$ appears in it:

If a sentence of monadic predicate logic (without identity) is satisfiable, then it has a model of size no greater than $2^k$ , where $k$ is the number of predicates in the sentence. (Lemma 21.8 BBJ).

As we’ve seen, $2^k$ is the number of possible combinations of predicates that can be true of a constant in the domain. Visually, this is the number of subsets in a partition of the possibility space:

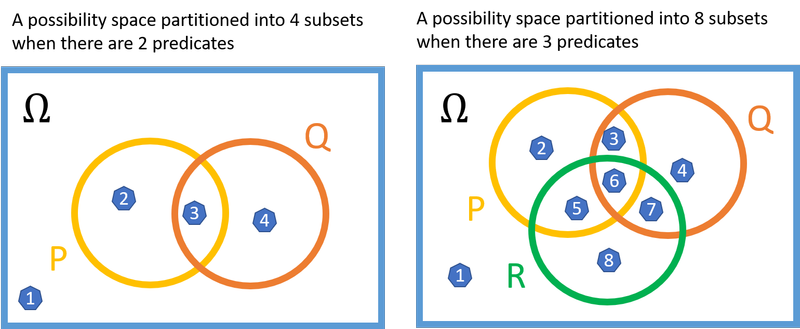
If a model had a size of, say, $2^k + 1$, one of the subsets in the partition would need to contain more than one element. But this additional element would be superfluous insofar as the truth-value of the sentence is concerned. The partition subset corresponds to a predicate-combination that would already be true with just one element in the subset, and will continue to be true if more elements are added. Take, for example, the subset labeled ‘8’ in the drawing, which corresponds to $R \land \neg Q \land \neg P$. The sentence $\exists x R(x) \land \neg Q(x) \land \neg P(x)$ is true whether there are one, two, or a million elements in subset 8. Similarly, $\forall x R(x) \land \neg Q(x) \land \neg P(x)$ does not depend on the number of elements in subset 8.

Seeing this not only illuminates the theorem, but also let us see that the vast majority of the multitudinous $\sum_{m=1}^{2^k} (2^k)^m$ models we considered earlier are equivalent. All that matters for our sentence’s truth-value is whether each of the subsets is empty or non-empty. This means there are in fact only $2^{(2^k)}-1$ model equivalence classes to consider. We need to subtract one because the subsets cannot all be empty, since the domain needs to be non-empty.

>>> k = 2
>>> eq_classes = [i for i in itertools.product(['Empty','Non-empty'],repeat=2**k)]
>>> eq_classes.remove(('Empty',)*k**2)
>>> eq_classes
[('Empty', 'Empty', 'Empty', 'Non-empty'),
 ('Empty', 'Empty', 'Non-empty', 'Empty'),
 ('Empty', 'Empty', 'Non-empty', 'Non-empty'),
 ('Empty', 'Non-empty', 'Empty', 'Empty'),
 ('Empty', 'Non-empty', 'Empty', 'Non-empty'),
 ('Empty', 'Non-empty', 'Non-empty', 'Empty'),
 ('Empty', 'Non-empty', 'Non-empty', 'Non-empty'),
 ('Non-empty', 'Empty', 'Empty', 'Empty'),
 ('Non-empty', 'Empty', 'Empty', 'Non-empty'),
 ('Non-empty', 'Empty', 'Non-empty', 'Empty'),
 ('Non-empty', 'Empty', 'Non-empty', 'Non-empty'),
 ('Non-empty', 'Non-empty', 'Empty', 'Empty'),
 ('Non-empty', 'Non-empty', 'Empty', 'Non-empty'),
 ('Non-empty', 'Non-empty', 'Non-empty', 'Empty'),
 ('Non-empty', 'Non-empty', 'Non-empty', 'Non-empty')]

We are now ready to consider the extension to monadic predicate logic with identity. With identity, it’s possible to check whether any two members of a model are distinct or identical. This means we can distinguish the case where a partition subset contains one element from the case where it contains several. But we can still only distinguish up to a certain number of elements in a subset. That number is bounded above by the number of variables in the sentence¹ (e.g. if you only have two variables $x$ and $y$, it’s not possible to construct a sentence that asserts there are three different things in some subset). Indeed we have:

If a sentence of monadic predicate logic with identity is satisfiable, then it has a model of size no greater than $2^k \times r$, where $k$ is the number of monadic predicates and $r$ the number of variables in the sentence. (Lemma 21.9 BBJ)

By analogous reasoning to the case without identity, we need only consider $(r+1)^{(2^k)}-1$ model equivalence classes. All that matters for our sentence’s truth-value is whether each of the subsets has $0, 1, 2 ...$ or $r$ elements in it.

>>> k = 2
>>> r = 2
>>> eq_classes = [i for i in itertools.product(range(r+1),repeat=2**k)]
>>> eq_classes.remove((0,)*k**2)
>>> eq_classes
[(0, 0, 0, 1),
 (0, 0, 0, 2),
 (0, 0, 1, 0),
 (0, 0, 1, 1),
 (0, 0, 1, 2),
 (0, 0, 2, 0),
 (0, 0, 2, 1),
 (0, 0, 2, 2),
 (0, 1, 0, 0),
 (0, 1, 0, 1),
 (0, 1, 0, 2),
 (0, 1, 1, 0),
 (0, 1, 1, 1),
...

The index fund company Vanguard supports two-factor authentication (2fa) with SMS. SMS is known to be the worst form of 2fa, because it is vulnerable to so-called SIM-swapping attacks. In this type of attack, the malicious party impersonates you and tells your telephone company you’ve lost your SIM card. They request that your number be moved to a new SIM card that they possess. The attacker could call up the company and ask them to activate a spare SIM card that they’ve acquired earlier, or they could visit a store and ask to be given a new SIM card for your number. Then they can receive your security codes.

The security of SMS-based 2fa is only as good as your phone operator’s protections against SIM-swapping, meaning probably not very good. The attacker only needs to convince one mall telco shop employee that they’re you, and they can likely try as many times as they want.

Vanguard claims to also support hardware security keys as a second factor. These are widely regarded as the gold standard for 2fa. Not only are they a true piece of hardware that can’t be SIM-swapped, they also ensure you’re protected even if you get fooled by a phishing attempt (by sending a code that is a function of the URL you are on).

So good news, right? No, because Vanguard made the inexplicable decision to force everyone who uses a security key to also keep SMS 2fa enabled as a fallback option. This utterly defeats the point. The attacker can just click ‘lost security key’ and get an SMS code instead. Users who enable the security key feature actually make their account less secure, because it now has two possible attack surfaces instead of one.

People have been complaining about this for years, ever since Vanguard first introduced security keys. On the Bogleheads forum (where intense Vanguard fanatics congregate), this issue was recognized in this thread from 2016, this one from 2017, this one from 2018, and several others. There are plenty of complaints on reddit too. It’s fair to assume some of these people will have contacted Vanguard directly too.

It’s disappointing that a company with over 6 trillion dollars of assets under management offers its clients a security “feature” that makes their accounts less secure.

The workaround I’ve found is to use a Google Voice number to receive SMS 2fa codes (don’t bother with the useless security key). Of course, you must set the Google Voice number not to forward SMS messages to your main phone number, which would defeat the purpose. Then, the messages can only be read by being logged in to the Google account. A Google account can be made into an extremely hardened target. The advanced protection program is available for the sufficiently paranoid.

If you don’t receive the SMS for some reason, you can also receive the authentication code with an automated call to the same number.

You need to have an existing US phone number to create a Google Voice account.

By the way, using Google Voice may not work for all companies that force you to use SMS 2fa. I have verified that it works for Vanguard. This poster claims that “many financial institutions will now only send their 2FA codes to true mobile phone numbers. Google Voice numbers are land lines, with the text messaging function spliced on via a third-party messaging gateway”.

We often have intuitions about the probability distribution of a variable that we would like to translate into a formal specification of a distribution. Transforming our beliefs into a fully specified probability distribution allows us to further manipulate the distribution in useful ways.

For example, you believe that the cost of a medication is a positive number that’s about 10, but with a long right tail: say, a 10% probability of being more than 100. To use this cost estimate in a Monte Carlo simulation, you need to know exactly what distribution to plug in. Or perhaps you have a prior about the effect of creatine on cognitive performance, and you want to formally update that prior using Bayes’ rule when a new study comes out. Or you want to make a forecast about a candidate’s share of the vote and evaluate the accuracy of your forecast using a scoring rule.

In most software, you have to specify a distribution by its parameters, but these parameters are rarely intuitive. The normal distribution’s mean and standard deviation are somewhat intuitive, but this is the exception rather than the rule. The lognormal’s mu and sigma correspond to the mean and standard deviation of the variable’s logarithm, something I personally have no intuitions about. And I don’t expect good results if you ask someone to supply a beta distribution’s alpha and beta shape parameters.

I have built a tool that creates a probability distribution (of a given family) from user-supplied quantiles, sometimes also called percentiles. Quantiles are points on the cumulative distribution function: $(p,x)$ pairs such that $P(X<x)=p$. To illustrate what quantiles are, we can look at the example distribution below, which has a 50th percentile (or median) of -1 and a 90th percentile of 10.

A cumulative distribution function with a median of -1 and a 90th percentile of 10

The code is on GitHub, and the webapp is here.

Let’s run through some examples of how you can use this tool. At the end, I will discuss how it compares to other probability elicitation software, and why I think it’s a valuable addition.

Traditional distributions

The tool supports the normal and lognormal distributions, and more of the usual distribution families could easily be added. The user supplies the distribution family, along with an arbitrary number of quantiles. If more quantiles are provided than the distribution has parameters (more than two in this case), the system is over-determined. The tool then uses least squares to find the best fit.

This is some example input:

family = 'lognormal'
quantiles = [(0.1,50),(0.5,70),(0.75,100),(0.9,150)]

And the corresponding output:

More than two quantiles provided, using least squares fit

Lognormal distribution
mu 4.313122980928514
sigma 0.409687416531683

quantiles:
0.01 28.79055927521217
0.1 44.17183774344628
0.25 56.64439363937313
0.5 74.67332855521319
0.75 98.44056294458953
0.9 126.2366766332274
0.99 193.67827989071688

Metalog distribution

The feature I am most excited about, however, is the support for a new type of distribution developed specifically for the purposes of flexible elicitation from quantiles, called the meta-logistic distribution. It was first described in Keelin 2016, which puts it at the cutting edge compared to the venerable normal distribution invented by Gauss and Laplace around 1810. The meta-logistic, or metalog for short, does not use traditional parameters. Instead, it can take on as many terms as the user provides quantiles, and adopts whatever shape is needed to fit these quantiles very closely. Closed-form expressions exist for its quantile function (the inverse of the CDF) and for its PDF. This leads to attractive computational properties (see footnote)¹.

Keelin explains that

[t]he metalog distributions provide a convenient way to translate CDF data into smooth, continuous, closed-from distribution functions that can be used for real-time feedback to experts about the implications of their probability assessments.

The metalog quantile function is derived by modifying the logistic quantile function,

by letting $\mu$ and $s$ depend on $y$ instead of being constant.

As Keelin writes, given a systematically increasing $s$ as one moves from left to right, a right skewed distribution would result. And a systematically decreasing $\mu$ as one moves from left to right would make the distribution spikier in the middle with correspondingly heavier tails.

By modifying $s$ and $\mu$ in ever more complex ways we can make the metalog take on almost any shape. In particular, in most cases the metalog CDF passes through all the provided quantiles exactly². Moreover, we can specify the metalog to be unbounded, to have arbitrary bounds, or to be semi-bounded above or below.

Instead of thinking about which of several highly constraining distribution families to use, just choose the metalog and let your quantiles speak for themselves. As Keelin says:

one needs a distribution that has flexibility far beyond that of traditional distributions – one that enables “the data to speak for itself” in contrast to imposing unexamined and possibly inappropriate shape constraints on that data.

For example, we can fit an unbounded metalog to the same quantiles as above:

family = 'metalog'
quantiles = [(0.1,50),(0.5,70),(0.75,100),(0.9,150)]
metalog_leftbound = None
metalog_rightbound = None

Meta-logistic distribution

quantiles:
0.01 11.968367580205552
0.1 50.000000000008185
0.25 58.750000000005215
0.5 70.0
0.75 100.00000000000519
0.9 150.00000000002515
0.99 281.7443263650518

The metalog’s actual parameters (as opposed to the user-supplied quantiles) have no simple interpretation and are of no use unless the next piece of software you’re going to use knows what a metalog is. Therefore the program doesn’t return the parameters. Instead, if we want to manipulate this distribution, we can use the expressions of the PDF and CDF that the software provides, or alternatively export a large number of samples into another tool that accepts distributions described by a list of samples (such as the Monte Carlo simulation tool Guesstimate). By default, 5000 samples will be printed; you can copy and paste them.

Approaches to elicitation

How does this tool compare to other approaches for creating subjective belief distributions? Here are the strategies I’ve seen.

Belief intervals

The first approach is to provide a belief interval that is mapped to some fixed quantiles, e.g. a 90% belief interval (between the 0.05 and 0.95 quantile) like on Guesstimate. Metaculus provides a graphical way to input the same data, allowing the user to drag the quantiles across a line under a graph of the PDF. This is the simplest and most user-friendly approach. The tool I built incorporates the belief interval approach while going beyond it in two ways. First, you can provide completely arbitrary quantiles, instead of specifically the 0.05 and 0.95 – or some other belief interval symmetric around 0.5. Second, you can provide more than two quantiles, which allows the user to query intuitive information about more parts of the distribution.

Guesstimate

Metaculus

Drawing

Another option is to draw the PDF on a canvas, in free form, using your mouse. This is the very innovative approach of probability.dev.³

probability.dev

Ought’s elicit

Ought’s elicit lets you provide quantiles like my tool, or equivalently bins with some probability mass in each bin⁴. The resulting distribution is by default piecewise uniform (the cdf is piecewise linear), but it’s possible to apply smoothing. It has all the features I want, the drawback is that it only supports bounded distributions⁵.

Elicit

Mixtures

A meta-level approach that can be applied to any of the above is to allow the user to specify a mixture distribution, a weighted average of distributions. For example, 1/3 weight on a normal(5,5) and 2/3 weight on a lognormal(1,0.75). My opinion on mixtures is that they are good if the user is thinking about the event disjunctively; for example, she may be envisioning two possible scenarios, each of which she has a distribution in mind for. But on Metaculus and Foretold my impression is that mixtures are often used to indirectly achieve a single distribution whose rough shape the user had in mind originally.

The future

This is an exciting space with many recent developments. Guesstimate, Metaculus, Elicit and the metalog distribution have all been created in the last 5 years.